In this article, you will learn the implementation of Kruskal’s Algorithm in C programming and starting with Kruskal’s Algorithm.
Kruskal’s Algorithm
It is a greedy algorithm that is directly based on MST (Minimum Spanning Tree). Kruskal’s algorithm finds a minimum spanning tree for a connected weighted graph.
It finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized.
There are many fields where Kruskal’s Algorithm is practically used such as in the field of Traveling Salesman Problem, Creating Mazes and Computer Networks, etc.
Minimum Spanning Tree
A Minimum Spanning Tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree whose sum of edge weights is as small as possible.
Number of edges in a Minimum Spanning Tree (MST): (V-1)
here, V is the number of vertices in the given graph.
C Programming Implementation of Kruskal’s Algorithm
Source Code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 | #include <stdio.h> #include <conio.h> #include <stdlib.h> int i, j, k, a, b, u, v, n, ne = 1; int min, mincost = 0, cost[9][9], parent[9]; int find(int); int uni(int, int); void main() { printf("Kruskal's algorithm in C\n"); printf("========================\n"); printf("Enter the no. of vertices:\n"); scanf("%d", &n); printf("\nEnter the cost adjacency matrix:\n"); for (i = 1; i <= n; i++) { for (j = 1; j <= n; j++) { scanf("%d", &cost[i][j]); if (cost[i][j] == 0) cost[i][j] = 999; } } printf("The edges of Minimum Cost Spanning Tree are\n"); while (ne < n) { for (i = 1, min = 999; i <= n; i++) { for (j = 1; j <= n; j++) { if (cost[i][j] < min) { min = cost[i][j]; a = u = i; b = v = j; } } } u = find(u); v = find(v); if (uni(u, v)) { printf("%d edge (%d,%d) =%d\n", ne++, a, b, min); mincost += min; } cost[a][b] = cost[b][a] = 999; } printf("\nMinimum cost = %d\n", mincost); getch(); } int find(int i) { while (parent[i]) i = parent[i]; return i; } int uni(int i, int j) { if (i != j) { parent[j] = i; return 1; } return 0; } |
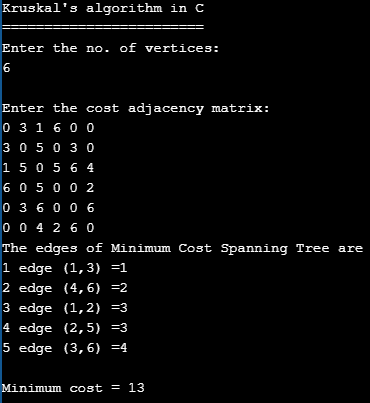
The output of Kruskal’s Algorithm implementation in C.
Time Complexity of Kruskal’s Algorithm.
The time complexity of the algorithm= O (e log e) + O (e log n)
where, e is the number of edges.
n is the number of vertices.O (e log e) is sorting algorithm’s time complexity.O (e log n) is the merging of components’ time complexity.
