In this tutorial, you will learn to write a program to find the inverse of a matrix in C. Let us first start by understanding how to find the inverse of a matrix and the requirements to find it.
In order to find the inverse of a matrix,
- The matrix must be a square matrix.
- Determinant needs to be calculated and should not equal to zero (0).
- Then find the adjoint of a matrix and
- Lastly, multiply 1/determinant by adjoint to get the inverse of a matrix.
Adjoint of a matrix
The adjoint of a matrix is obtained by taking the transpose of the cofactor matrix of a given square matrix. it is also called the Adjugate matrix. For matrix A, it is denoted by adj A.
Determinant of a matrix:
It is calculated in the following way for the square matrices.

The formula to find inverse of matrix:
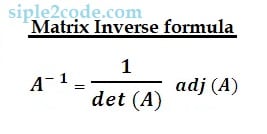
C Program to Find Inverse of a Matrix
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 | #include<stdio.h> #include<math.h> //function prototype that are being created void cofactor(float [][25], float); float determinant(float [][25], float); void transpose(float [][25], float [][25], float); int main() { float a[25][25], n, d; int i, j; printf("Enter the order of the Matrix: "); scanf("%f", &n); printf("Enter the elements of a matrix: \n"); for (i = 0;i < n; i++) { for (j = 0;j < n; j++) { scanf("%f", &a[i][j]); } } d = determinant(a, n); if (d == 0) printf("Since the determinant is zerp (0), therefor inverse is not possible."); else cofactor(a, n); } // function for the calculation of determinant float determinant(float a[25][25], float k) { float s = 1, det = 0, b[25][25]; int i, j, m, n, c; if (k == 1) { return (a[0][0]); } else { det = 0; for (c = 0; c < k; c++) { m = 0; n = 0; for (i = 0;i < k; i++) { for (j = 0 ;j < k; j++) { b[i][j] = 0; if (i != 0 && j != c) { b[m][n] = a[i][j]; if (n < (k - 2)) n++; else { n = 0; m++; } } } } det = det + s * (a[0][c] * determinant(b, k - 1)); s = -1 * s; } } return (det); } // function for cofactor calculation void cofactor(float num[25][25], float f) { float b[25][25], fac[25][25]; int p, q, m, n, i, j; for (q = 0;q < f; q++) { for (p = 0;p < f; p++) { m = 0; n = 0; for (i = 0;i < f; i++) { for (j = 0;j < f; j++) { if (i != q && j != p) { b[m][n] = num[i][j]; if (n < (f - 2)) n++; else { n = 0; m++; } } } } fac[q][p] = pow(-1, q + p) * determinant(b, f - 1); } } transpose(num, fac, f); } ///function to find the transpose of a matrix void transpose(float num[25][25], float fac[25][25], float r) { int i, j; float b[25][25], inverse[25][25], d; for (i = 0;i < r; i++) { for (j = 0;j < r; j++) { b[i][j] = fac[j][i]; } } d = determinant(num, r); for (i = 0;i < r; i++) { for (j = 0;j < r; j++) { inverse[i][j] = b[i][j] / d; } } printf("\nThe inverse of matrix: \n"); for (i = 0;i < r; i++) { for (j = 0;j < r; j++) { printf("\t%f", inverse[i][j]); } printf("\n"); } } |
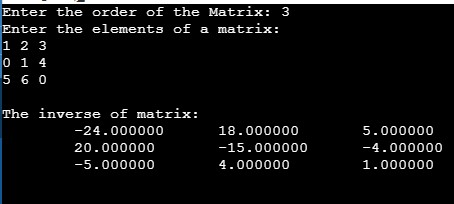
Output: