Simple2Code

Heap Sort in Java

Written by

admin

in

In this tutorial, we will learn how to implement Heap Sort in java. First, we will start by understanding the Heap Sort algorithm.

Heap Sort Algorithm

Heap is a tree in heap sorting that possesses some specific properties whose value should be greater than or equal to that of the children node.

Heapsort is a comparison-based sorting algorithm and is also considered as the improved Selection sort. It is based on a Binary Heap data structure so to understand we must know two types of data structure:
Arrays and trees

What is Binary heap?

Complete Binary tree:
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

Binary Heap:
A binary heap is a complete binary tree where the parent node is greater than its two children node.

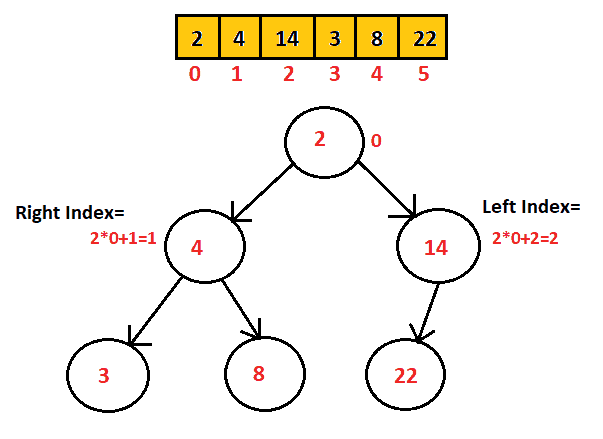
Representation of Binary tree:
Considering the height of a tree be “h“, then:

  • Index of left child = 2*(index of its parent)+1
  • Index of right child = 2*(index of its parent)+2
Binary heap

Types of heaps:

  • Min heap
  • Max heap

Min heap and max heap are the binary heaps that represent the ordering of an array.

  • Min heap: In this binary heap, the value of the parent node is always greater than its child node.
  • Max heap: In this binary heap, the value of the parent node is always less than its child node.

A heap sorting algorithm for increasing order:

  • First, create a max Heap from the input array.
  • Replace the root element (which has the largest element) with the last element in the array. Then heapify the root of the tree.
  • Now repeat the steps until all elements are sorted in an array.

A heap sorting algorithm for decreasing order.

  • First, create a min Heap from the input array.
  • Replace the root element (which has the smallest element) with the last element in the array. Then heapify the root of the tree.
  • Now repeat the steps until all elements are sorted in an array.

Before we begin, you need to have an idea of the following:

Time Complexity of Heap Sort:

  • Best case:  0(nlogn)
  • Average case:  0(nlogn)
  • Worst case:  0(nlogn)

Java Program to implement heap sort

import java.util.Arrays;

public class HeapSortAlgo
{
  public void sort(int arrA[])
  {
    int size = arrA.length;

    // create heap
    for (int i = size / 2 - 1; i >= 0; i--)
      heapify(arrA, size, i);

    //Replacement of element
    for (int i = size - 1; i >= 0; i--)
    {
      //arrA[0] being max element
      int x = arrA[0];
      arrA[0] = arrA[i];
      arrA[i] = x;

      // call max
      heapify(arrA, i, 0);
    }
  }

  void heapify(int arrA[], int heapSize, int i)
  {
    // Initializing
    int largest = i;
    //Indexes
    int leftChild = 2 *i + 1;
    int rightChild = 2 *i + 2;

    // If left child is larger than root
    if (leftChild < heapSize && arrA[leftChild] > arrA[largest])
      largest = leftChild;

    //if right child is larger than root
    if (rightChild < heapSize && arrA[rightChild] > arrA[largest])
      largest = rightChild;

    // If root is not largest
    if (largest != i)
    {
      int swap = arrA[i];
      arrA[i] = arrA[largest];
      arrA[largest] = swap;

      // Recursive call
      heapify(arrA, heapSize, largest);
    }
  }

  public static void main(String args[])
  {
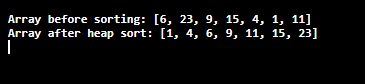
    int arrA[] = { 6, 23, 9, 15, 4, 1, 11 };

    System.out.println("Array before sorting: " + Arrays.toString(arrA));
    HeapSortAlgo heapSort = new HeapSortAlgo();
    heapSort.sort(arrA);

    System.out.println("Array after heap sort: " + Arrays.toString(arrA));
  }
}

The output of Heap sorting in Java:

More posts