In this article, we will learn about Sparse matrix, its use and its different representation.
What is a sparse matrix?
A matrix can be defined with a 2-dimensional array with column m and row n represented as m * n matrix. However, there may be a matrix or matrices that may contain less Non-Zero values than Zero values. Such a matrix is known as the Sparse matrix.
We can say that it is a matrix that contains a few Non-Zero elements.
Why use Sparse Matrix instead of a simple matrix?
There are mainly two reasons:
- Storage: Sparse matrix allows us to use the memory to store only non-zero elements. So, less storage is required.
- Computing time: designing a data- structure that traverses only Non-Zero elements, computing time can be saved.
Sparse Matrix Representation:
There are two ways to represent a sparse matrix:
- Triplet Representation(Array Representation)
- Linked Representation
1. Triplet Representation(Array Representation)
It is an array representation where only Non-Zero elements are store in three rows named as:
- Row: This contains an index number for a row where non-zero elements are situated.
- Column: This contains an index number for a column where the non-zero element is stored.
- Value: These contain all the values of Non-Zero elements located at their respective index i.e. rows and columns.
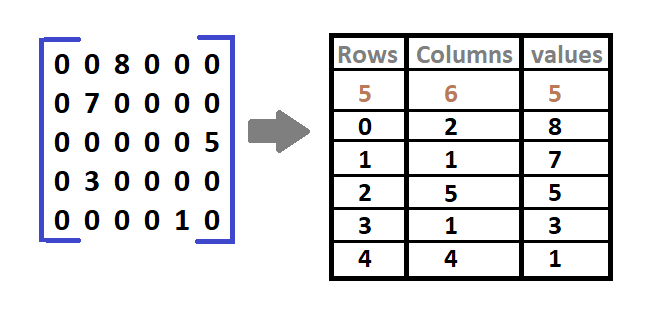
In the above diagram of matrix size 5* 6, there are 5 non-zero elements (8, 7, 5, 3, 1). The right-hand side table indicates it’s a sparse matrix with Rows, Columns, and Values. Values are the non-zero elements that are present in their particular row and column. Eg. 0th row and 2nd column contain the non-zero element 8 in the sparse matrix. Ans the following shows a similar pattern.
Triplet Representation(Array Representation) using C++
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | #include<iostream> using namespace std; int main() { // sparse matrix of class 5x6 with 6 non-zero values int sparseMatrix[5][6] = { {0 , 0 , 0 , 0 , 4, 0 }, {0 , 6 , 0 , 0 , 0, 0 }, {0 , 4 , 0 , 0 , 0, 1 }, {0 , 0 , 0 , 0 , 0, 5 }, {0 , 0 , 9 , 0 , 0, 0 } }; // Looking for non-zero values in the sparse matrix int size = 0; for (int row = 0; row < 5; row++){ for (int column = 0; column < 6; column++){ if (sparseMatrix[row][column] != 0){ size++; } } } //result Matrix int resultMat[3][size]; int k = 0; for (int row = 0; row < 5; row++) for (int column = 0; column < 6; column++) if (sparseMatrix[row][column] != 0) { resultMat[0][k] = row; resultMat[1][k] = column; resultMat[2][k] = sparseMatrix[row][column]; k++; } // Displaying result cout<<"Triplet Representation of Sparse Matrix : "<<endl; for (int row=0; row<3; row++) { for (int column = 0; column<size; column++) cout<<resultMat[row][column]<<" "; cout<<endl; } return 0; } |
Output of sparse matrix using C++:
1 2 3 4 | Triplet Representation of Sparse Matrix : 0 1 2 2 3 4 4 1 1 5 5 2 4 6 4 1 5 9 |
2. Linked List Representation:
The Linked list data structure is used to represent a sparse matrix.
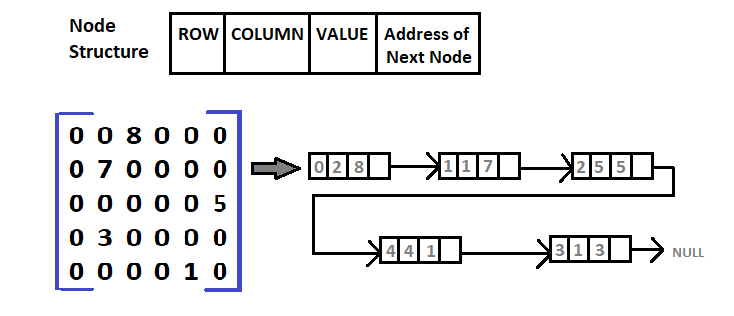
Here, each node has four fields and they are:
- Row: This contains an index number for a row where non-zero elements are situated.
- Column: This contains an index number for a column where a non-zero element is stored.
- Value: These contain all the values of Non-Zero elements located at their respective index i.e. rows and columns.
- Next Node: This contains the address of the next node.
C Program to determine if a given matrix is in a sparse matrix or not.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | //(Remainder) Sparse matrix has more zero values than non-zero values. #include <stdio.h> void main () { static int arr[20][20]; int i, j, m, n; int counter = 0; printf("Enter the order of the matix \n"); scanf("%d %d", &m, &n); printf("Enter the matix \n"); for (i = 0; i < m; ++i) { for (j = 0; j < n; ++j) { scanf("%d", &array[i][j]); if (arr[i][j] == 0) { ++counter; } } } if (counter > ((m * n) / 2)) { printf("The given matrix is a sparse matrix \n"); } else printf("The given matrix is not a sparse matrix \n"); printf("Number of zeros is %d", counter); } |
Output of sparse matrix using C:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | Enter the order of the matix 3 3 Enter the matix 0 2 0 0 5 0 6 0 0 The given matrix is a sparse matrix Number of zeros is 6 |
