In this tutorial, we will learn about the algorithms in C language with examples and practices. Let us start by understanding algorithms.
What is Algorithm?
An algorithm is a set of well-defined instructions to solve a particular problem. It is a step-by-step procedure to execute some instructions in a certain order to get the required output. Software Engineer commonly uses an algorithm for planning and solving problems.
Following are the characteristics of an Algorithm:
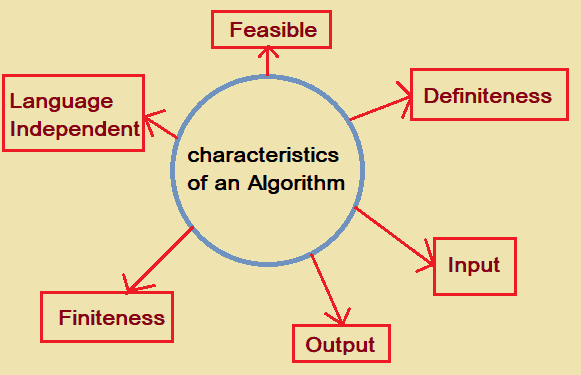
- Definiteness: Each instruction must be clear and unambiguous.
- Input: An algorithm may have 0(zero) inputs or may have well-defined inputs.
- Output: Each algorithm is expected to produce one or more than one desired output.
- Finiteness: once the algorithm is executed, the algorithm must terminate after a finite number of steps.
- Language Independent: The direction of steps in an algorithm should be independent of any programming language.
- Feasible: The algorithm should be simple and generic so that it is feasible with any available resources.
How to write algorithm in C or for any other languages.
As told earlier, algorithm is independent of any programming language, so there is no well-defined method to write an algorithm. It depends on your problem and resources.
However, you may need to have a basic understanding on writing algorithms. Follow the steps below.
- Define your algorithm’s input.
- Define the variables.
- Outline the algorithm’s operations.
- Output the results of your algorithm’s operations.
There are some common types of control structures that are used while writing an algorithm such as Branching (if-else statements), loops (do-while, for, while), or in a sequence structure that is execution taking place starting from up to down.
Advantages of Algorithm
- It is easy to understand because of its step-wise representation.
- As it is independent of programming language so the person with no programming language can understand it.
- The procedural step helps the problem to break down into smaller problems, making it easier for the programmer to understand and code.
Example of algorithms
Problem 1: write an algorithm to add two numbers and display the result.
Step 1: START
Step 2: Declare integer variables num1, num2, and result.
Step 3: Read values num1 and num2.
Step 4: add the value and store it to the result variable. result←num1+num2
Step 5: print result
Step 6: STOP
Problem 2: write an algorithm to calculate the factorial of a number and print the result.
Step 1: START
Step 2: Declare num, fact, and i.
Step 3: Initialize fact=1 and i=1
Step 4: Read n
Step 5: if i <= num go to step 6 else go to step 8
Step 6: Calculate fact = fact * i
Step 7: i++ and go to step 5
Step 8: Print fact
Step 9: STOP
Analysis of Algorithm
There are two ways to analyze an algorithm that is before implementation and after implementation. They are:
1. Priori Analysis: The meaning of Priori is before, hence indicating that this analysis is done before the implementation of an algorithm. It is a theoretical analysis step. This Efficiency of an algorithm is measured by assuming that all other factors, for example, processor speed, are constant and have no effect on the implementation. The algorithm designer is responsible for this analysis.
2. Posterior Analysis: Here Posterior means after, hence indicating that this analysis is done after the implementation of an algorithm. Here the checking of an algorithm is done by implementing it in any programming language. The programmer checks the statistics like running time, correctness, space required, etc.
Complexity of an algorithm
The time and space are the two main factors that decides the complexity of the algorithm.
Time factor: This time factor of an algorithm is calculated by counting the number of key operations such as comparisons in the sorting algorithm.
Space Factor: This space factor of an algorithm is calculated by counting the maximum memory space required by the algorithm.
Space Complexity
Space complexity refers to the amount of memory that an algorithm uses in its life cycle to get the result. The calculation of space complexity is done on the basis of the following two components.
- Fixed Part: This space is required by the algorithm to store input variables, output variables, program size, etc. those size are independent of the problem
- Variable Part: This is the space required to store variables that are dependent on the size of the problem. For example, temporary variables, dynamic memory allocation, recursion stack space, etc.
Time Complexity
Time complexity refers to the amount of time that an algorithm required in its life cycle for the completion of the task. This can be for the operations, conditional if-else statements, etc. The calculation of space complexity is done on the basis of the following two components.
- Constant time part: Instruction that is executed only once such as input, output, if-else, switch, etc.
- Variable Time Part: Instruction that is executed more than once such as loops, recursion, etc.